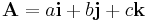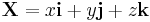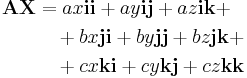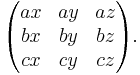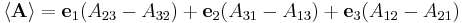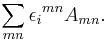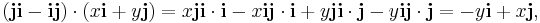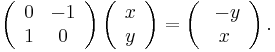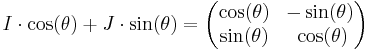Dyadic tensor

In multilinear algebra, a dyadic is a second rank tensor written in a special notation, formed by juxtaposing pairs of vectors, along with a notation for manipulating such expressions analogous to the rules for matrix algebra.

Each component of a dyadic is a dyad. A dyad is the juxtaposition of a pair of basis vectors and a scalar coefficient. As an example, let

\mathbf{A} = a \mathbf{i} %2B b \mathbf{j} %2B c \mathbf{k}
\mathbf{X} = x \mathbf{i} %2B y \mathbf{j} %2B z\mathbf{k}

be a pair of three-dimensional vectors. Then the juxtaposition of A and X is

\begin{align} \mathbf{A X} &= a x \mathbf{i i} %2B a y \mathbf{i j} %2B a z \mathbf{i k} %2B \\ &\quad %2Bb x \mathbf{j i} %2B b y \mathbf{j j} %2B b z \mathbf{j k}%2B\\ &\quad %2B c x \mathbf{k i} %2B c y \mathbf{k j} %2B c z \mathbf{k k} \end{align}

each monomial of which is a dyad. This dyadic can be represented as a 3×3 matrix

\begin{pmatrix} ax & ay & az\\ bx & by & bz\\ cx & cy & cz \end{pmatrix}.

Contents

Definition

Following Morse & Feshbach (1953), a dyadic (in three dimensions) is a 3×3 array of components Aij, i,j = 1,2,3 expressed in coordinates that satisfy a covariant transformation law when passing from one coordinate system to another:

(A_{ij})' = \sum_{m,n} \frac{\partial x_m}{\partial x_i'}\frac{\partial x_n}{\partial x_j'} A_{mn}.

Thus a dyadic is a covariant tensor of order two.

The dyadic itself, rather than its components, is referred to by a boldface letter A = (Aij).

Operations on dyadics

A dyadic A can be combined with a vector v by means of the dot product:

\mathbf{A}\cdot\mathbf{v} = \sum_{m,n} \mathbf{e}_mA_{mn}v_n

where the vectors ei denote the coordinate basis. The resulting expression transforms like a covariant vector. This suggests employing the notation

\begin{align} \mathbf{A} &= A_{11}\mathbf{e}_1\mathbf{e}_1%2BA_{12}\mathbf{e}_1\mathbf{e}_2%2BA_{13}\mathbf{e}_1\mathbf{e}_3 %2B\\ &\quad %2BA_{21}\mathbf{e}_2\mathbf{e}_1 %2B A_{22}\mathbf{e}_2\mathbf{e}_2%2B A_{23}\mathbf{e}_2\mathbf{e}_3\\ &\quad %2BA_{31}\mathbf{e}_3\mathbf{e}_1 %2B A_{32}\mathbf{e}_3\mathbf{e}_2%2B A_{33}\mathbf{e}_3\mathbf{e}_3. \end{align}

so that the dot product associates with the juxtaposition of vectors.

The tensor contraction of a dyadic

|\mathbf{A}| = \sum_m A_m^m

is the spur or expansion factor. It arises from the formal expansion of the dyadic in a coordinate basis by replacing each juxtaposition by a dot product of vectors. In three dimensions only, the rotation factor

\langle\mathbf{A}\rangle = \mathbf{e}_1(A_{23}-A_{32})%2B\mathbf{e}_2(A_{31}-A_{13}) %2B \mathbf{e}_3(A_{12}-A_{21})

arises by replacing every juxtaposition by a cross product. The resulting vector is the complete contraction of A with the Levi-Civita tensor:

\sum_{mn}{\epsilon_i}^{mn}A_{mn}.

Examples

The dyadic tensor

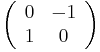
J = j i − i j = \left( \begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array} \right)

is a 90° rotation operator in two dimensions. It can be dotted (from the left) with a vector to produce the rotation:

(\mathbf{j i} - \mathbf{i j}) \cdot (x \mathbf{i} %2B y \mathbf{j}) = x \mathbf{j i} \cdot \mathbf{i} - x \mathbf{i j} \cdot \mathbf{i} %2B y \mathbf{j i} \cdot \mathbf{j} - y \mathbf{i j} \cdot \mathbf{j} = -y \mathbf{i} %2B x \mathbf{j},

or in matrix notation

\left( \begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array} \right)\left( \begin{array}{c} x \\ y \end{array} \right)=\left( \begin{array}{c} \ -y \\ x \end{array} \right).

A General 2-D Rotation Dyadic for \theta angle, anti-clockwise

I\cdot\cos(\theta) %2B J\cdot\sin(\theta)= \begin{pmatrix} \cos(\theta) &-\sin(\theta) \\ \sin(\theta) &\;\cos(\theta) \end{pmatrix}

The identity dyadic tensor in three dimensions is

I = i i + j j + k k = iTi + jTj + kTk.

This can be put on more careful foundations (explaining what the logical content of "juxtaposing notation" could possibly mean) using the language of tensor products. If V is a finite-dimensional vector space, a dyadic tensor on V is an elementary tensor in the tensor product of V with its dual space. The tensor product of V and its dual space is isomorphic to the space of linear maps from V to V: a dyadic tensor vf is simply the linear map sending any w in V to f(w)v. When V is Euclidean n-space, we can (and do) use the inner product to identify the dual space with V itself, making a dyadic tensor an elementary tensor product of two vectors in Euclidean space. In this sense, the dyadic tensor i j is the function from 3-space to itself sending ai + bj + ck to bi, and j j sends this sum to bj. Now it is revealed in what (precise) sense i i + j j + k k is the identity: it sends ai + bj + ck to itself because its effect is to sum each unit vector in the standard basis scaled by the coefficient of the vector in that basis.

See also

Notes

References